transformation matrix for points translations
Rotation
For rotation by an angle θ clockwise about the origin, the functional form is 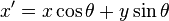 and
and  . Written in matrix form, this becomes:
. Written in matrix form, this becomes:
Similarly, for a rotation counter clockwise about the origin, the functional form is  and
and  and the matrix form is:
and the matrix form is:
 and
and  and the matrix form is:
and the matrix form is:Scaling
For scaling (that is, enlarging or shrinking), we have  and
and  . The matrix form is:
. The matrix form is:
When  , no change in size
, no change in size
 , no change in size
, no change in size
when > 1 , size increases
when < 1 , size decreases
Shearing
For shear mapping (visually similar to slanting), there are two possibilities.
A shear parallel to the x axis has  and
and  . Written in matrix form, this becomes:
. Written in matrix form, this becomes:
 and
and  . Written in matrix form, this becomes:
. Written in matrix form, this becomes:
A shear parallel to the y axis has  and
and  , which has matrix form:
, which has matrix form:
 and
and  , which has matrix form:
, which has matrix form: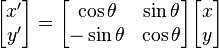




Comments
Post a Comment